---
title: "Основи прикладної статистики для аналітиків"
subtitle: "Лекція з практичними прикладами на Python"
author: "Богдан Красюк"
date: "2025-10-20"
lang: uk
categories: ["Лекції", "Аналітика даних"]
format:
html:
toc: true
toc-location: right
math: mathjax
toc-title: "План лекції"
toc-depth: 3
number-sections: true
code-fold: show
code-tools: true
smooth-scroll: true
execute:
echo: true
warning: false
message: false
---
## 🎯 Навчальні цілі
Після цієї лекції ви зможете:
- розрізняти **генеральну сукупність** і **вибірку**, **параметри** і **статистики**;
- добирати коректні **описові метрики** та **візуалізації**;
- пояснювати роль **випадковості**, **похибок** і **упереджень**;
- будувати **довірчі інтервали** та тлумачити їх без помилок;
- формулювати та перевіряти **статистичні гіпотези**, розуміти **помилки I/II роду** і **потужність**;
- критично оцінювати **дизайн дослідження** та дотримуватися **етики** й **відтворюваності**.
::: callout-note
**Формат**: короткі теорблоки + практика в Python (синтетичні приклади, щоб сфокусуватись на методології).
:::
## 🧩 Базові поняття
::: callout-note
**Навіщо це знати?** Щоб узгодити терміни та уникати категоріальних помилок (наприклад, застосовувати середнє до номінальної змінної). Коректна ідентифікація *сукупність→вибірка* та *параметр→статистика* визначає тип оцінювання й валідації.
:::
::: callout-tip
**Як це працює?** Ми моделюємо реальний світ як сукупність із невідомими параметрами $\theta$. Спостерігаємо вибірку $X_1,\dots,X_n$ і обчислюємо статистики $T(X)$, які служать оцінками для $\theta$. Тип шкали (номінальна/порядкова/інтервальна/відносна) задає дозволені операції й метрики.
:::
::: callout-important
**Де і коли використовувати?** На етапі проєктування схеми даних, формування метрик, перед EDA й перед вибором тестів/моделей; у документації до датасетів (data contracts).
:::
**Термінологія**
- **Генеральна сукупність** $\mathcal{P}$: вся множина об’єктів інтересу (напр., усі запити до API).
- **Вибірка** $\{x_i\}_{i=1}^n$: підмножина спостережень з $\mathcal{P}$.
- **Параметри** $\theta$: числа, що описують $\mathcal{P}$ (напр., $\mu, \sigma^2$).
- **Статистики** $T(X)$: функції від вибірки (напр., $\bar{x}, s^2$).
**Шкали вимірювання**
- *Номінальна* (категорії без порядку), *порядкова* (є порядок, але немає сталої різниці),
*інтервальна* (стала різниця, немає абсолютного нуля; напр., °C), *відносна* (є нуль і відношення; напр., час, маса).
Тип шкали визначає дозволені перетворення і валідні статистичні операції.
**Фінальна вибіркова модель**
- **Рамка вибірки** (sampling frame) і випадковий механізм відбору.
- **Скінченна корекція** (FPC) при відборі без повернення: $\mathrm{SE}_{\text{FPC}} = \mathrm{SE}\cdot \sqrt{\tfrac{N-n}{N-1}}$.
## 📊 Описова статистика та візуалізації
::: callout-note
**Навіщо це знати?** Описова статистика стискає великі обсяги даних до кількох зрозумілих чисел/графіків, допомагає виявляти викиди, аномалії та формувати гіпотези.
:::
::: callout-tip
**Як це працює?** Ми порівнюємо робастні (медіана, IQR, MAD) й чутливі (mean, sd) метрики та дивимось на *форму* розподілу (асиметрія, ексцес). Візуалізації підбираються за типом змінних.
:::
::: callout-important
**Де і коли використовувати?** На етапі EDA, у моніторингу (SLA/SLO), у звітності, при узгодженні шкал і перетворень (лог, Box–Cox).
:::
**Центр і розсіювання**
- Середнє: $\bar{x}=\tfrac{1}{n}\sum x_i$.
- Медіана — стійка до викидів; **триміноване середнє** $\bar{x}_{\alpha}$ (обрізання $\alpha$ з кожного краю).
- Дисперсія/СКВ: $s^2=\tfrac{1}{n-1}\sum (x_i-\bar{x})^2,\ s=\sqrt{s^2}$.
- **MAD** (median absolute deviation): $\mathrm{MAD} = \mathrm{median}(|x_i - \mathrm{median}(x)|)$ — робастна шкала.
**Форма розподілу**
- Асиметрія: $\mathrm{skew} = \tfrac{1}{n}\sum \big(\tfrac{x_i-\bar{x}}{s}\big)^3$.
- Ексцес (надмірна опуклість): $\mathrm{kurt} = \tfrac{1}{n}\sum \big(\tfrac{x_i-\bar{x}}{s}\big)^4 - 3$.
- Викиди (правило Тьюкі): точка є викидом, якщо $x<Q_1-1.5\cdot \mathrm{IQR}$ або $x>Q_3+1.5\cdot \mathrm{IQR}$.
**Перетворення змінних**
- Лог, Box–Cox, Yeo–Johnson — для стабілізації дисперсії, зменшення асиметрії, лінеаризації зв’язків.
```{python}
import numpy as np, pandas as pd, matplotlib.pyplot as plt
rng = np.random.default_rng(42)
lat = rng.normal(120, 25, size=300)
lat = np.clip(lat, 40, None)
df = pd.DataFrame({"latency_ms": lat})
summary = df.describe(percentiles=[.25,.5,.75]).T
summary[["mean","std","25%","50%","75%"]]
```
```{python}
#| label: fig-latency-hist
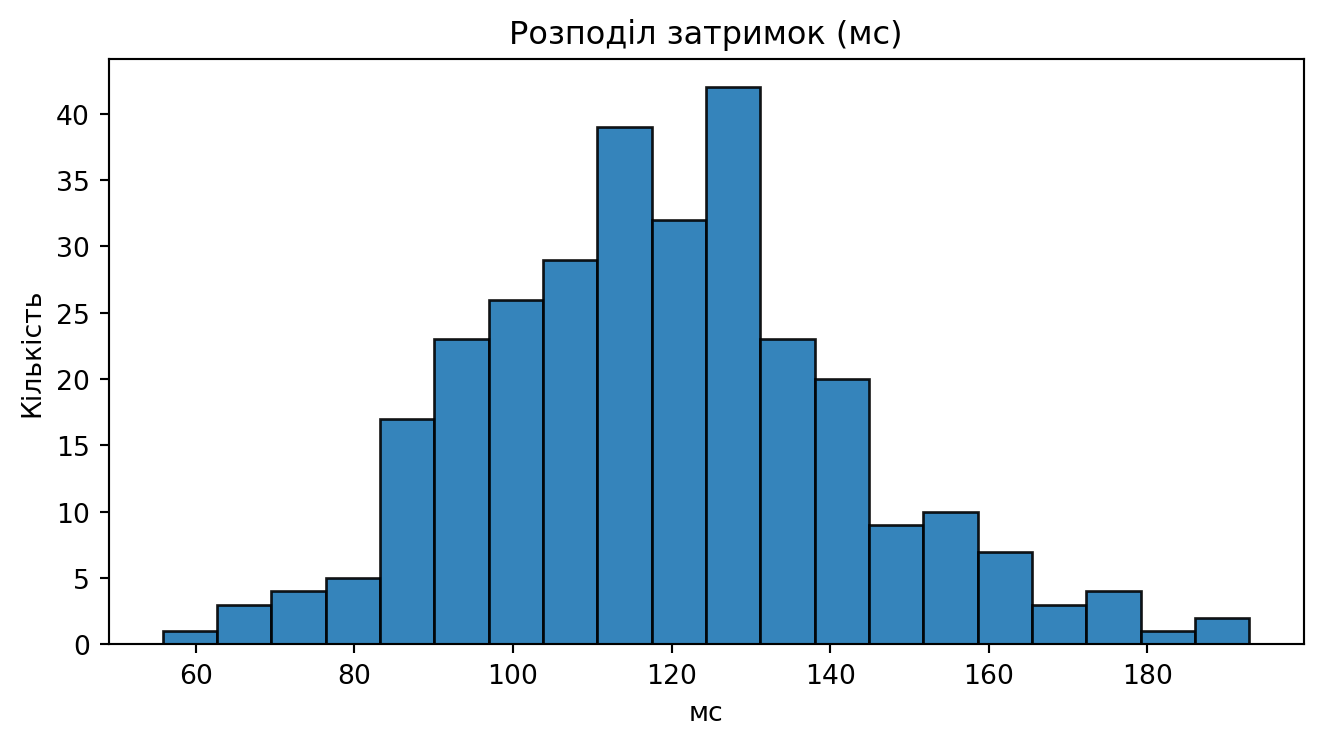
#| fig-cap: "Гістограма затримок (мс)"
plt.figure(figsize=(7,4))
plt.hist(lat, bins=20, edgecolor="black", alpha=0.9)
plt.title("Розподіл затримок (мс)")
plt.xlabel("мс"); plt.ylabel("Кількість")
plt.tight_layout(); plt.show()
```
```{python}
#| label: fig-latency-box
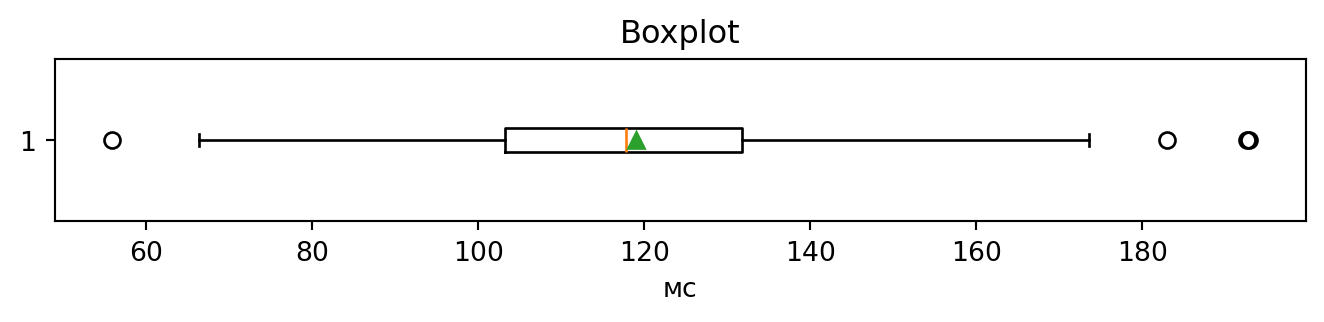
#| fig-cap: "Boxplot затримок (мс)"
plt.figure(figsize=(7,1.8))
plt.boxplot(lat, vert=False, showmeans=True)
plt.xlabel("мс"); plt.title("Boxplot")
plt.tight_layout(); plt.show()
```
::: callout-tip
**Правило добору діаграм:** категоріальна → bar/stacked bar; кількісна → гістограма/щільність, boxplot; дві кількісні → scatter.
:::
## 🧪 Якість даних і похибки
::: callout-note
**Навіщо це знати?** Якість даних визначає валідність висновків. Упередження відбору чи вимірювання можуть повністю зруйнувати інференцію.
:::
::: callout-tip
**Як це працює?** Пропуски класифікуємо як MCAR/MAR/MNAR і обираємо стратегію (від видалення до мультиімпутації). Вимірювальна похибка у предикторах зменшує оцінені зв’язки (attenuation).
:::
::: callout-important
**Де і коли використовувати?** Опитування, телеметрія, логування, A/B‑експерименти, ETL‑пайплайни з пропусками чи змінами схем.
:::
**Класи похибок**
- *Випадкова* (шум) vs *систематична* (зміщення). Систематичні: *selection*, *non-response*, *survivorship*, *measurement*.
- Наслідок вимірювальної похибки в регресії — **послаблення** коефіцієнтів (attenuation).
**Пропуски**
- **MCAR**: пропуски незалежні від даних; **MAR**: залежать від спостережуваних; **MNAR**: залежать від неспостережуваних.
- Стратегії: видалення списків (OK при MCAR), проста/багаторазова імпутація, модельно-орієнтовані підходи.
```{python}
# Демонстрація пропусків та простої імпутації середнім
lat_nan = lat.copy()
missing_idx = rng.choice(len(lat_nan), 20, replace=False)
lat_nan[missing_idx] = np.nan
share_missing = np.mean(np.isnan(lat_nan))
lat_imputed = np.where(np.isnan(lat_nan), np.nanmean(lat_nan), lat_nan)
print(f"Частка пропусків: {share_missing:.2%}")
print(f"Середнє до/після імпутації: {np.nanmean(lat_nan):.2f} -> {lat_imputed.mean():.2f}")
```
## 🎲 Ймовірність та розподіли
::: callout-note
**Навіщо це знати?** Ймовірність — фундамент для моделювання ризиків, симуляцій і статистичних висновків.
:::
::: callout-tip
**Як це працює?** Через аксіоми Колмогорова, умовну ймовірність і формулу Байєса описуємо невизначеність; ЦГТ пояснює, чому багато статистик мають наближено нормальний розподіл.
:::
::: callout-important
**Де і коли використовувати?** Оцінка SLA‑ризиків, моделі черг/навантаження, детектування аномалій, планування пропускної здатності.
:::
**Аксіоми Колмогорова**
- Імовірність $P(A)\in[0,1]$; $P(\Omega)=1$; для несумісних $A,B$: $P(A\cup B)=P(A)+P(B)$.
**Незалежність і умовна імовірність**
- $A\perp B \iff P(A\cap B)=P(A)P(B)$.
- $P(A|B)=\tfrac{P(A\cap B)}{P(B)}$ (за $P(B)>0$).
- **Повна імовірність** і **Баєс**:
\[P(B)=\sum_i P(B|A_i)P(A_i),\quad P(A|B)=\frac{P(B|A)P(A)}{P(B)}.\]
**Класичні розподіли**
- Біноміальний: $X\sim\mathrm{Bin}(n,p)$, $\mathbb{E}X=np$, $\mathrm{Var}X=np(1-p)$.
- Нормальний: $\mathcal{N}(\mu,\sigma^2)$. t, $\chi^2$, F — сімейство для вибіркових метрик.
**Закони великих чисел і ЦГТ**
- СЗВЧ: $\bar{X}_n \to \mu$ за ймовірністю.
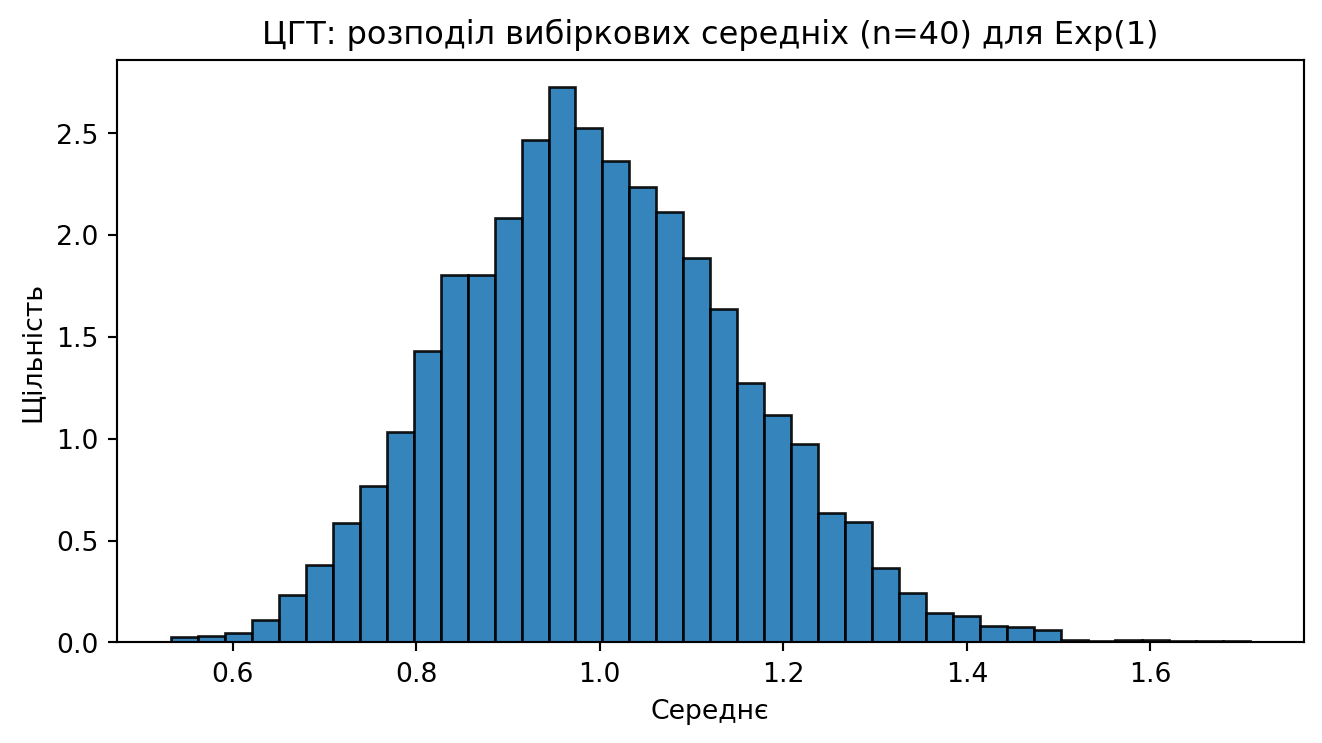
- ЦГТ: $\sqrt{n}(\bar{X}-\mu)/\sigma \Rightarrow \mathcal{N}(0,1)$. У практиці — достатній $n$ і обмежені «хвости».
```{python}
# ЦГТ: середні з експоненціального розподілу
samples = rng.exponential(scale=1.0, size=(5000, 40)) # 5000 вибірок по n=40
means = samples.mean(axis=1)
import matplotlib.pyplot as plt
plt.figure(figsize=(7,4))
plt.hist(means, bins=40, density=True, edgecolor="black", alpha=0.9)
plt.title("ЦГТ: розподіл вибіркових середніх (n=40) для Exp(1)")
plt.xlabel("Середнє"); plt.ylabel("Щільність")
plt.tight_layout(); plt.show()
```
## 📏 Оцінювання та довірчі інтервали
::: callout-note
**Навіщо це знати?** ДІ кількісно описують *невизначеність* оцінок — ключ до обґрунтованих бізнес‑рішень і порівнянь.
:::
::: callout-tip
**Як це працює?** Стандартна похибка визначає ширину інтервалу; використовуємо t‑інтервали для середніх, Wilson/Agresti–Coull — для часток; для дисперсії — $\chi^2$‑інтервали. Плануємо $n$ під бажану похибку.
:::
::: callout-important
**Де і коли використовувати?** Звіти по KPI, контроль якості, порівняння релізів/версій, планування вибірки до запуску експерименту.
:::
**Властивості оцінок**
- *Незміщеність*: $\mathbb{E}[\hat{\theta}]=\theta$.
- *Консистентність*: $\hat{\theta}\xrightarrow{P}\theta$.
- *Ефективність*: мінімальна дисперсія серед незміщених (границя Крамера–Рао).
**Методи отримання оцінок**
- Метод моментів (MoM), метод максимальної правдоподібності (MLE).
- Робастні оцінки (медіана, MAD) — при відхиленнях від нормальності.
**ДІ для середнього (невідоме $\sigma$)**
$$
\bar{x}\pm t_{1-\alpha/2,\,n-1}\frac{s}{\sqrt{n}}.
$$
**ДІ для частки $p$**: рекомендований **Wilson** або **Agresti–Coull**, а не «Wald»:
$$
\hat{p}_{\text{Wilson}}=\frac{\hat{p}+\frac{z^2}{2n}}{1+\frac{z^2}{n}},\quad
\mathrm{SE}_{\text{Wilson}}=\frac{\sqrt{\frac{\hat{p}(1-\hat{p})}{n}+ \frac{z^2}{4n^2}}}{1+\frac{z^2}{n}}.
$$
**ДІ для дисперсії (нормальність):**
$$
\frac{(n-1)s^2}{\chi^2_{1-\alpha/2,\,n-1}} \le \sigma^2 \le \frac{(n-1)s^2}{\chi^2_{\alpha/2,\,n-1}}.
$$
**Планування вибірки (накидки)**
- Для середнього: $n \approx \big(\tfrac{z_{1-\alpha/2}\,\sigma}{\mathrm{ME}}\big)^2$.
- Для частки: $n \approx \tfrac{z_{1-\alpha/2}^2\,\hat{p}(1-\hat{p})}{\mathrm{ME}^2}$.
```{python}
from scipy import stats
n = len(lat)
xbar = np.mean(lat)
s = np.std(lat, ddof=1)
alpha = 0.05
tcrit = stats.t.ppf(1 - alpha/2, df=n-1)
margin = tcrit * s / np.sqrt(n)
ci = (xbar - margin, xbar + margin)
print(f"x̄ = {xbar:.2f}, s = {s:.2f}, n = {n}")
print(f"95% ДІ для середнього: ({ci[0]:.2f}, {ci[1]:.2f})")
```
::: callout-important
**Інтерпретація ДІ**: у **95%** однотипних вибірок, збудовані інтервали накриватимуть істинне $\mu$. Це **не** ймовірність для конкретного інтервалу.
:::
## 🧪 Гіпотези, помилки та потужність
::: callout-note
**Навіщо це знати?** Щоб уникати хибнопозитивних/хибнонегативних висновків і планувати адекватну потужність тестів.
:::
::: callout-tip
**Як це працює?** Визначаємо $H_0/H_A$, обираємо статистику, фіксуємо $\alpha$, рахуємо p‑value та/або ДІ; обов’язково оцінюємо розмір ефекту (Cohen’s $d$, OR, RR). Для нерівних дисперсій — Welch’s t‑тест; для еквівалентності — TOST.
:::
::: callout-important
**Де і коли використовувати?** A/B‑тести, медичні/поведінкові дослідження, порівняння моделей/алгоритмів, контроль регресій у продукті.
:::
**Процедура тестування**
1) сформулювати $H_0$ і $H_A$
2) обрати статистику
3) визначити рівень $\alpha$;
4) розрахувати p-value
5) зробити висновок
6) оцінити **розмір ефекту** і побудувати ДІ.
**Помилки і потужність**
- Помилка I роду $\alpha$, помилка II роду $\beta$; **потужність** $1-\beta$.
- **Розмір ефекту**: Cohen’s $d$, Hedges’ $g$, $r$, **відношення шансів** (OR), **ризик** (RR), **ARR**, **NNT**.
**Зв’язок ДІ і тестів**: якщо 0 не входить у ДІ для різниці, двосторонній тест (на тому ж $\alpha$) відхиляє $H_0$.
```{python}
# Двовибірковий t-тест (Welch)
A = rng.normal(120, 25, size=200) # контроль
B = rng.normal(115, 25, size=200) # варіант
tstat, pval = stats.ttest_ind(A, B, equal_var=False)
pooled_sd = np.sqrt((A.var(ddof=1) + B.var(ddof=1))/2)
d = (A.mean() - B.mean()) / pooled_sd
print(f"t = {tstat:.2f}, p = {pval:.4f}, d = {d:.3f}")
```
## 🅰️/🅱️ Міні-кейс: тест часток (конверсії)
::: callout-note
**Навіщо це знати?** Порівнювати конверсії/події між варіантами — базовий інструмент продуктового розвитку.
:::
::: callout-tip
**Як це працює?** Використовуємо Z‑тест із пулінгом під $H_0$, будуємо ДІ для різниці пропорцій, перевіряємо припущення незалежності та відсутності перетинів трафіку; уникаємо *optional stopping*.
:::
::: callout-important
**Де і коли використовувати?** Запуск нових UI/фіч, email‑кампаній, paywall‑експериментів; у фіче‑флагах і поетапних релізах.
:::
**Модель**
- $H_0: p_A=p_B$ проти $H_A: p_A\ne p_B$ (двосторонній) або $p_B>p_A$ (односторонній).
- Передумови: незалежні випробування, стабільна популяція, відсутність перетинів трафіку, єдина метрика успіху.
**Z-тест із пулінгом**
- $\hat{p}=\dfrac{x_A+x_B}{n_A+n_B}$,
$\mathrm{SE}=\sqrt{\hat{p}(1-\hat{p})(\tfrac{1}{n_A}+\tfrac{1}{n_B})}$,
$z=\dfrac{\hat{p}_B-\hat{p}_A}{\mathrm{SE}}$.
**Практика**
- Плануйте $n$ під очікувану мінімальну детектовану різницю (MDE).
- Уникайте *optional stopping*; для проміжних аналізів — поправки (O’Brien–Fleming, Pocock).
```{python}
nA, nB = 500, 500
convA = rng.binomial(1, 0.10, size=nA) # 10%
convB = rng.binomial(1, 0.13, size=nB) # 13%
pA, pB = convA.mean(), convB.mean()
p_pool = (convA.sum() + convB.sum()) / (nA + nB)
se = np.sqrt(p_pool*(1-p_pool)*(1/nA + 1/nB))
z = (pB - pA)/se
p_two = 2*(1 - stats.norm.cdf(abs(z)))
# 95% ДІ для різниці часток (без пулінгу, нормальна апроксимація)
se_unpooled = np.sqrt(pA*(1-pA)/nA + pB*(1-pB)/nB)
zcrit = stats.norm.ppf(0.975)
ci = ((pB-pA) - zcrit*se_unpooled, (pB-pA) + zcrit*se_unpooled)
print(f"pA={pA:.3f}, pB={pB:.3f}, diff={pB-pA:.3f}")
print(f"z={z:.2f}, p(two-sided)={p_two:.4f}")
print(f"95% ДІ для (pB - pA): ({ci[0]:.3f}, {ci[1]:.3f})")
```
## 🧮 Мультиперевірки (оглядово)
::: callout-note
**Навіщо це знати?** Багато паралельних тестів різко збільшують шанс хибних відкриттів.
:::
::: callout-tip
**Як це працює?** Контролюємо FWER (Bonferroni/Holm) або FDR (Benjamini–Hochberg). Вибір залежить від ціни хибних позитивів.
:::
::: callout-important
**Де і коли використовувати?** Панелі метрик, відбір ознак, моніторинги з багатьма сигналами, багатоваріантні експерименти.
:::
- Багато тестів ⇒ зростає **FWER** (family-wise error rate).
- Підходи: Bonferroni/Holm (контроль FWER), **Benjamini–Hochberg** (контроль **FDR**).
::: callout-tip
**BH-FDR (есенція):** відсортуйте p‑value $p_{(1)}\le\dots\le p_{(m)}$ і знайдіть найбільший $k$, для якого
$p_{(k)} \le \tfrac{k}{m}q$. Відхиліть $H_{(1)},\dots,H_{(k)}$.
:::
## 🧭 Дизайн досліджень, причинність та етика
::: callout-note
**Навіщо це знати?** Гарний дизайн визначає причинну інтерпретацію та довіру до результатів.
:::
::: callout-tip
**Як це працює?** Рандомізація, блокування/стратифікація, сліпі дизайни, DAG‑мислення та пре‑реєстрація зменшують упередження та p‑hacking.
:::
::: callout-important
**Де і коли використовувати?** Користувацькі дослідження, медичні/соціальні випробування, оцінка політик, складні змішані дизайни у продуктах.
:::
- **Спостережні** (крос‑секційні, панельні, кейс‑контроль) vs **експериментальні** (РКД).
- **Confounding**: змінні, що впливають і на експозицію, і на результат. Інструменти: рандомізація, стратифікація/блокування, регресійне коригування, DAG‑мислення.
- **Відтворюваність**: пре‑реєстрація гіпотез, протоколи збору, контроль версій даних/коду, відкриті матеріали.
- **Етика**: згода, приватність, мінімізація ризиків, чесне звітування (включно з негативними результатами).
::: callout-warning
Статистична значущість ≠ практична значущість. Оцінюйте **розмір ефекту** й вплив на продукт/користувача.
:::
## ✅ Підсумок
- Дані → Модель → Висновок: помилки можливі на кожному кроці.
- Перевіряйте **припущення**, **дизайн**, **розмір ефекту**, **узагальнюваність**.
- В A/B — плануйте $n$ під **MDE**, контролюйте **FDR/FWER**, уникайте *p‑hacking*.
## 🧠 Глосарій термінів
- **Генеральна сукупність** — повна множина об’єктів або подій, про які хочемо зробити висновок.
- **Вибірка** — підмножина спостережень, фактично зібраних з генеральної сукупності.
- **Параметр** — фіксована, але невідома характеристика сукупності (наприклад, середнє або дисперсія населення).
- **Статистика** — числова характеристика вибірки (наприклад, вибіркове середнє або вибіркова дисперсія).
- **Номінальна шкала** — категорії без природного порядку.
- **Порядкова шкала** — категорії з порядком, але без сталої різниці між рівнями.
- **Інтервальна шкала** — числова шкала зі сталою різницею, але без абсолютного нуля (наприклад, градуси Цельсія).
- **Відносна шкала** — числова шкала з абсолютним нулем і змістовними відношеннями (наприклад, маса, час).
- **Середнє (mean)** — сума значень, поділена на кількість спостережень.
- **Медіана (median)** — центральне значення впорядкованих даних; робастна до викидів.
- **Мода (mode)** — найчастіше значення у даних.
- **Дисперсія** — середній квадрат відхилення значень від середнього; характеризує розсіювання.
- **Стандартне відхилення (СКВ)** — квадратний корінь з дисперсії; масштаб розсіювання у тих самих одиницях, що й дані.
- **IQR (міжквартильний розмах)** — різниця між 75-м та 25-м перцентилями; робастна міра розсіювання.
- **MAD** — медіана абсолютних відхилень від медіани; робастна міра розсіювання.
- **Асиметрія (skewness)** — міра відхилення розподілу від симетрії.
- **Ексцес (kurtosis)** — міра «гостроверхості» або «плосковерхості» розподілу порівняно з нормальним.
- **Викид** — спостереження, яке істотно відрізняється від інших і може бути результатом помилки або рідкісної події.
- **Перетворення змінних** — математичні трансформації (логарифм, Box–Cox, Yeo–Johnson), що стабілізують дисперсію або роблять розподіл ближчим до симетричного.
- **Випадкова похибка** — неконтрольований шум вимірювання або відбору, що не має системного зміщення.
- **Систематична похибка (bias)** — стабільне зміщення оцінки через помилки дизайну чи вимірювання.
- **Selection bias** — упередження, спричинене невипадковим відбором одиниць у вибірку.
- **Non-response bias** — упередження, коли ненадання відповідей пов’язане з досліджуваною величиною.
- **Survivorship bias** — спотворення через фокус на «тих, хто вижив» і ігнорування відсіяних випадків.
- **Measurement error** — похибка, що виникає під час вимірювання змінних.
- **MCAR/MAR/MNAR** — класи механізмів пропусків: випадкові незалежно від даних; залежні від спостережуваних; залежні від неспостережуваних.
- **Випадкова величина** — змінна, значення якої визначається випадковим експериментом.
- **Математичне сподівання** — теоретичне середнє значення випадкової величини.
- **Дисперсія сукупності** — середній квадрат відхилення випадкової величини від її математичного сподівання.
- **Незалежність подій** — відсутність впливу результату однієї події на іншу.
- **Умовна ймовірність** — ймовірність події з урахуванням, що інша подія вже відбулася.
- **Формула повної ймовірності** — розклад ймовірності через повну групу несумісних подій.
- **Формула Байєса** — оновлення ймовірності гіпотези за наявності нових спостережень.
- **Закон великих чисел** — збіжність вибіркового середнього до очікуваного при зростанні обсягу вибірки.
- **Центральна гранична теорема** — нормальність розподілу вибіркового середнього для достатньо великих вибірок.
- **Точкова оцінка** — одиничне наближення невідомого параметра (наприклад, вибіркове середнє).
- **Стандартна похибка (SE)** — оцінка мінливості статистики від вибірки до вибірки.
- **Довірчий інтервал (ДІ)** — інтервал, який із заданою частотою покриває істинний параметр у повторних вибірках.
- **Рівень довіри** — частота покриття параметра побудованими інтервалами (наприклад, 95%).
- **t-розподіл** — розподіл статистик, що використовуються для середнього при невідомій дисперсії і малих вибірках.
- **t-критерій (t-тест)** — тест для порівняння середніх (одновибірковий, парний, двовибірковий).
- **p-value** — ймовірність спостерігати значення статистики не менш екстремальне за отримане, за умови істинності нульової гіпотези.
- **Помилка I роду** — відхилення істинної нульової гіпотези (хибне спрацьовування).
- **Помилка II роду** — не відхилення хибної нульової гіпотези (пропуск ефекту).
- **Потужність тесту** — ймовірність виявити справжній ефект (1 − β).
- **Розмір ефекту** — кількісна міра практичної різниці (наприклад, Cohen’s d, відношення шансів, відносний ризик).
- **A/B тест** — експериментальне порівняння двох варіантів (контроль і новий варіант) за заздалегідь визначеною метрикою.
- **Пулінг часток** — об’єднання даних груп для оцінювання дисперсії під нульовою гіпотезою у Z-тесті.
- **Z-тест для часток** — перевірка рівності часток у двох незалежних вибірках за нормальної апроксимації.
- **Wilson-інтервал** — рекомендований довірчий інтервал для частки з кращими властивостями покриття.
- **Agresti–Coull інтервал** — модифікація інтервалу для частки з покращеним покриттям порівняно з «класичним» Wald.
- **FWER** — імовірність хоча б однієї помилки I роду серед множини тестів.
- **FDR** — очікувана частка хибних спрацьовувань серед усіх відхилених гіпотез.
- **Benjamini–Hochberg процедура** — метод контролю FDR шляхом порівняння впорядкованих p-value з порогами.
- **Bonferroni/Holm поправки** — методи контролю FWER через коригування рівня значущості.
- **Confounding (змішування)** — спотворення зв’язку через третю змінну, що впливає і на причину, і на наслідок.
- **РКД (рандомізоване контрольоване дослідження)** — експеримент із випадковим розподілом у групи та контролем.
- **Рандомізація** — випадковий розподіл одиниць між умовами для усунення змішувальних факторів.
- **Стратифікація/блокування** — групування однорідних одиниць перед випадковим розподілом для зменшення варіативності.
- **DAG (орієнтований ациклічний граф)** — графічне подання причинно-наслідкових залежностей.
## 🏠 Домашнє завдання
1. Оберіть відкритий набір або згенеруйте синтетичні дані (≥ 200 рядків).
2. Визначте типи змінних і доречні діаграми (2–3 графіки).
3. Побудуйте 95% ДІ для середнього однієї кількісної змінної або для частки.
4. Сформулюйте і перевірте одну гіпотезу (t‑тест або тест часток); додайте **розмір ефекту**.
5. Коротко оцініть практичну значущість і можливі упередження.
6. Додатково (✳️): продемонструйте Wilson‑інтервал для частки.
## 📚 Список використаних джерел
- Agresti, A., & Coull, B. A. (1998). Approximate is better than “exact” for interval estimation of binomial proportions. *The American Statistician, 52*(2), 119–126.
- Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. *Journal of the Royal Statistical Society: Series B (Methodological), 57*(1), 289–300.
- Box, G. E. P., & Cox, D. R. (1964). An analysis of transformations. *Journal of the Royal Statistical Society: Series B (Methodological), 26*(2), 211–252.
- Casella, G., & Berger, R. L. (2002). *Statistical inference* (2nd ed.). Duxbury.
- Cohen, J. (1988). *Statistical power analysis for the behavioral sciences* (2nd ed.). Routledge.
- Efron, B., & Tibshirani, R. J. (1993). *An introduction to the bootstrap*. Chapman & Hall/CRC.
- Freedman, D., Pisani, R., & Purves, R. (2007). *Statistics* (4th ed.). W. W. Norton.
- Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013). *Bayesian data analysis* (3rd ed.). CRC Press.
- Montgomery, D. C. (2017). *Design and analysis of experiments* (9th ed.). Wiley.
- Rice, J. A. (2006). *Mathematical statistics and data analysis* (3rd ed.). Cengage.
- Wasserman, L. (2004). *All of statistics: A concise course in statistical inference*. Springer.
---
:::: {.columns}
::: {.column width="20%"}
<img src="https://kleban.page/bc-2025/images/logo.png" alt="Лого" style="height: 70px;">
:::
::: {.column width="30%"}
<img src="https://kleban.page/bc-2025/images/eu-founded.png" alt="Лого" style="height: 100px;">
:::
::: {.column width="50%"}
Проєкт реалізується за підтримки **Європейського Союзу** в межах програми [Дім Європи](https://houseofeurope.org.ua/).
:::
::::